企画名
| 理学における代数的手法 |
参加教員
| 教員名 | 所属 | 職名 |
|---|---|---|
| 石塚裕大(代表教員) | 数学・数理解析専攻 | MACS 特定助教 |
| 林重彦 | 化学専攻 | 教授 |
| 太田洋輝 | 物理学・宇宙物理学専攻 | MACS 特定助教 |
企画の概要
| グレブナー基底は連立多項式方程式を取り扱う、非常に普遍的なアルゴリズム(あるいはそれを提供する概念)である。本 SG では、グレブナー基底と統計を中心としたいくつかの話題を通じて、代数的な考え方や手法について学習し、その用法や計算機を用いた計算、そして自然科学においてあり得る応用について議論することが目標である。 具体的には、まず環論および統計において現れる各種の数学的概念を、計算機を用いた実習を通して学ぶ。その後、計算代数統計の初歩的なテキストの輪講を主軸として、発展や応用について議論する予定である。数学的概念の学習の際にも、理学の話題を提供することで動機を提供したいと考えている。 テキスト 青木 敏「計算代数統計 グレブナー基底と実験計画法」 |
実施期間・頻度
| 全年隔週 |
TA雇用の有無(講義型の場合には単位認定の有無)
有(大学院生から、希望者のみ)問い合わせ先
石塚 裕大 yasu-ishi*math.kyoto-u.ac.jp
(*を@に変えてください)
関心のある方は macs *sci.kyoto-u.ac.jp(*を@に変えてください)までご連絡ください。
活動報告
活動目的・内容
グレブナー基底は連立多項式方程式を取り扱う、非常に普遍的なアルゴリズム(あるいはそれを提供する概念)である。本 SG では、グレブナー基底と統計を中心としたいくつかの話題を通じて、代数的な考え方や手法について学習し、その用法や計算機を用いた計算、そして自然科学においてあり得る応用について議論することが目標である。
具体的には、まず環論および統計において現れる各種の数学的概念を、計算機を用いた実習を通して学ぶ。その後、計算代数統計の初歩的なテキストの輪講を主軸として、発展や応用について議論する予定である。数学的概念の学習の際にも、理学の話題を提供することで動機を提供したいと考えている。
テキスト
青木 敏「計算代数統計 グレブナー基底と実験計画法」
活動成果・自己評価
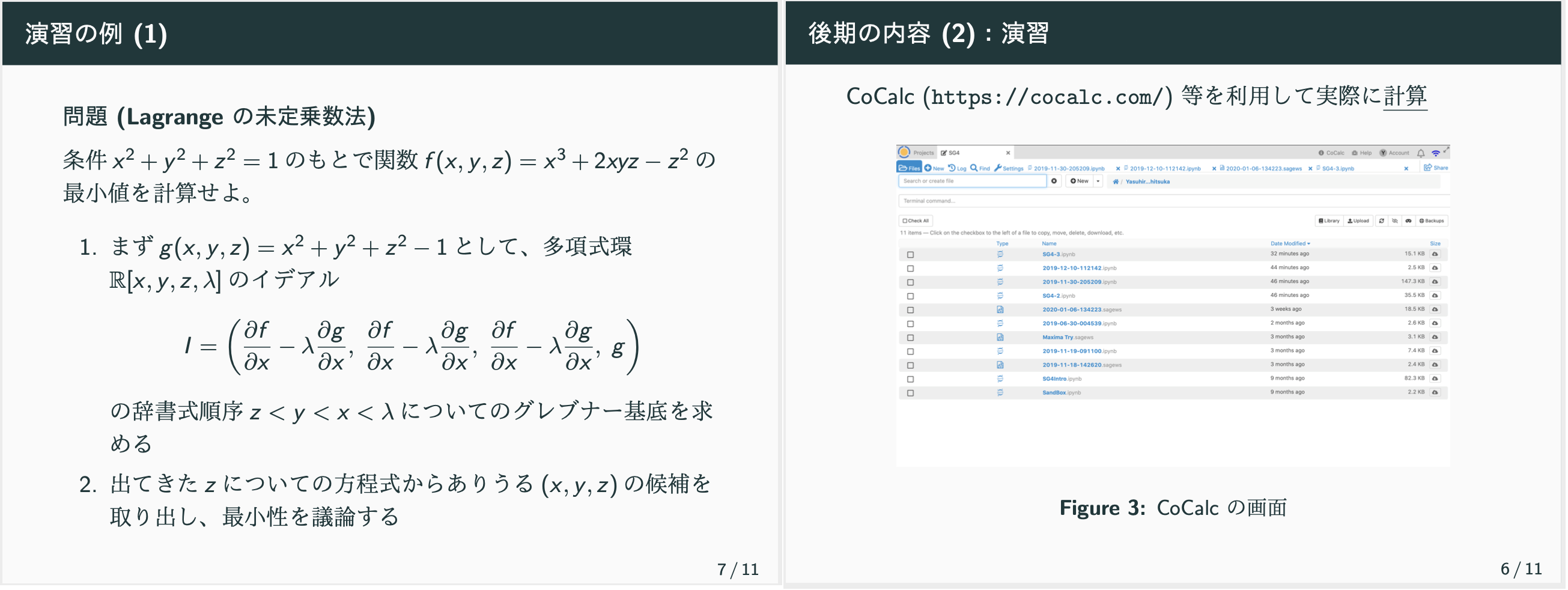
登録者は当初の想定より多く、教員5人、学生4名で行われた。理学部以外の参加者や、代数的な考え方に慣れていない参加者が確認できた。このため、前期はそれらの参加者に合わせる形で、多項式環やイデアル、グレブナー基底などの概念を学習した。使用した教科書は当初の予定通り青木氏の『計算代数統計』である。一方で代数的な取り扱いに比較的慣れた参加者がいることも想定して、参考文献を補い、また外部セミナーで神戸大学の小松瑞果氏に微分代数を用いた研究について紹介していただいた。後期は前期の知識をもとに実習を中心に講義を行い、残った参加者にはひとまずのグレブナー基底の利用法と、その計算ソフトの使用を教えることができた。ゆくゆくは参加者の問題意識につながることを期待したい。
反省点としては、前期のセミナーに少し時間を取りすぎたこと、および実習と輪講の並行した実施ができなかったことが挙げられる。利用したサービスについてのこちら側の準備不足が目立つ形となった。また、いくつかの素朴な問題意識は出たが、実質的な研究にはつながっていない。理学から少し目を離して、工学の非線形制御理論などの方面からも研究を紹介すると、より多くの問題意識に繋げられたかもしれないと感じている。
参加メンバー
| 氏名 | 所属 | 職名・学年 |
|---|---|---|
| 石塚 裕大(代表教員) | 数学・数理解析専攻 | MACS特定助教 |
| 林 重彦 | 化学専攻 | 教授 |
| 太田 洋輝 | 物理学・宇宙物理学専攻 | MACS特定助教 |
| 中野 直人 | 理学研究科 | 連携講師 |
| 塩崎 謙 | 物理学・宇宙物理学専攻 | 助教 |
| 太田 優希 | その他(理学研究科以外など) | B3 |
| 李 耀漢 | 化学専攻 | 研究生 |
| 別所 拓実 | 物理学・宇宙物理学専攻 | D1 |
| 高橋 直也 | 数学・数理解析専攻 | M2 |