物理学・宇宙物理学専攻(物理学第二分野)准教授 福間 将文

他の理学系研究分野と同様に物理学でも数値計算を用いた解析をよく行いますが、とくに重要なのは、多自由度系における力学変数の振る舞いを調べるため、与えられた作用汎関数(あるいはエネルギー汎関数)の下で物理量の期待値を計算することです。しかしながら巨視的な系の場合には、積分変数の数が巨大となるために多重数値積分を直接行うことができず、モンテカルロ法を用いて計算します。
実は、こうしたモンテカルロ法が直接使えるのは作用汎関数が実数値を取る場合だけで、複素数値を取る場合には激しい振動積分をモンテカルロ法で評価することになります。その際は、有限のサンプルサイズで様々な符号(より正確には様々な位相)の量を足し上げるために正確な値が得られにくく、実際、期待値を正しく評価するには自由度の指数関数という膨大な計算時間が必要となります。これが「符号問題」です。この問題は物理学に限定しても多くの重要な分野に登場し、典型的なものとしては、(核力などの強い力を記述する)量子色力学における有限密度系、高温超電導などの強相関電子系、場の量子論の実時間発展、などがあります。実際これまで、これらの問題の数値解析は符号問題のために絶望的に難しいとされてきました。
この符号問題に対し、最近、積分領域を実空間から複素空間の中へ連続変形し、レフシェッツ・シンブルと呼ばれる「作用汎関数の虚部が一定値を取る部分空間」の近傍でモンテカルロ計算を行うことが提案されました。とくに我々が開発した、変形パラメーターによる焼き戻し(tempering)によって符号問題とエルゴード問題を同時に解決する「tempered Lefschetz thimble法」は、ある程度自由度が大きな系に適用したときでも実用的な計算時間で正しい答えを与えることが確認されており、有力な方法となっています。今後は計算アルゴリズムのさらなる改良と計算機能力の向上により、上記の問題に対して遂にアプローチできる日が来ると考えています。
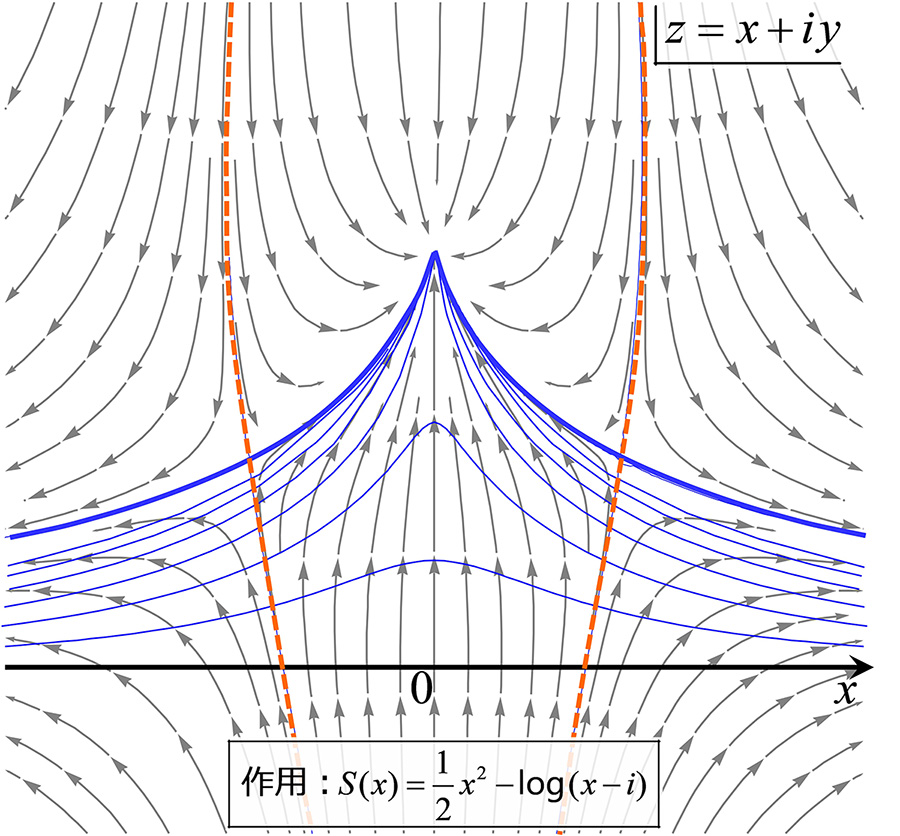
1自由度の場合の積分領域の連続変形(青太線がレフシェッツ・シンブル)



