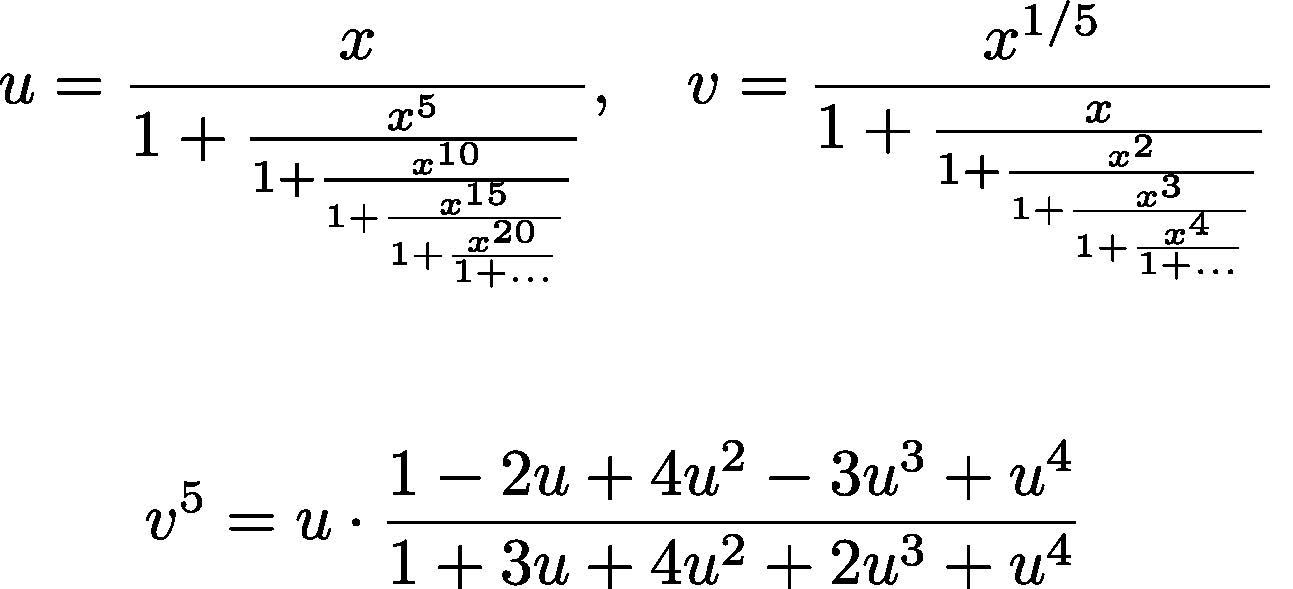数学の古い問題の一つに、与えられた方程式の整数解を求める問題がある。ＡＤ200年ごろの数学者ディオファントスにちなんでディオファントス問題と呼ばれる。二千年弱程研究されているが、あまり良く分かっていない。例として、オイラーが1769年に提案した次の方程式を考えてみる：

200年以上たって、Elkies(1988)は次の解を見つけた：

さて整数の問題ほど知名度はないが、関数に対するディオファントス問題というものがある。与えられた方程式を満たす関数を求める問題である。例えば、方程式

の解として次が見つかる：

もう少し面白い例としては、方程式　

の解として次が見つかる：

よりすごい例としては、20世紀初頭の天才ラマヌジャンが見つけたものがある（図1）。

関数に対するディオファントス問題も100年ほど研究されているが、あまり大きな理解には至っていない。私はここ10年ほど、この問題に対して力学系や情報理論を用いたアプローチを試みている。基本的な課題は、「与えられた方程式を満たす関数を記述するのに何ビット必要か？」である。いくつかの成果は得られているが、真に深い理解にたどり着けるかどうかはまだ分からない。

ところで、このような問題を研究することは何の役にたつのだろうか？私には明快な答えはない。ただ、ラマヌジャンの公式などを見ていると、これほど美しい物が役に立たないはずがないと素朴に感じる。